包子请加肉个人博客

Appearance

函数式编程 ​

函数式编程是一种编程范式，一种构建计算机程序结构和元素的方式，将计算视为数学函数的评估并避免改变状态和可变数据。

什么是函数式编程 ​

如果说面向对象核心是继承，那么函数式编程核心则是组合。

什么是组合？ ​

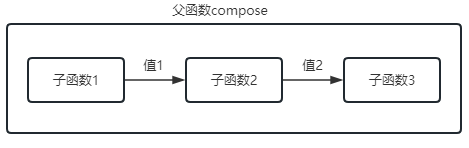
在编程中，组合就是把多个子函数合并成一个父级函数执行。当然这个组合会有一定的规则限制，不然这个组合就变的毫无意义。

  1. 子函数的执行必须按照组合的顺序执行
  2. 支持上一个子函数的结果传递到下一个函数

fnM

例如：实现一个商品总价打 8 折的功能

日常中我们这样写

js
const shop = [{ name: '糖果', price: 8}, { name: '书本', price: 20}]
const total = shop.reduce((price, item) => {
    return price + item.item
}, 0)
const sum = total * 0.8

虽然这是实现了效果，但是我们可以将其优化成组合函数来实现。首先我们需要将功能提取出来成单独的子函数

js
const shop = [{ name: '糖果', price: 8}, { name: '书本', price: 20}]

function countTotal = (arr) {
    return arr.reduce((price, item) => {
        return price + item.price
    }, 0)
}

function discounts8 = (price) {
    return price * 0.8
}

const total = countTotal(shop)
const sum = discounts8(total)

这一步我们提取出了两个子函数 countTotal 和 discounts8，然后分别调用来实现商品大致功能。但是由于没有把子函数组合起来所以还会存在一个问题。

那就是 countTotal 和 discounts8 执行之间可以存在执行代码空隙，而我们并不能确定这些代码是否能对我们结果是是否存在影响。例如修改了 total 的值。

为了解决这种可变性，所以我们需要实现一个组合函数 compose。使其形成管道式，就像水流过管道一样，通过一个个管口，并不被外界干扰。

js
const totalFn = compose(countTotal, discounts8)
totalFn(shop)

先不说函数 compose 的实现。这样实现的计算总价方式有两个优点：

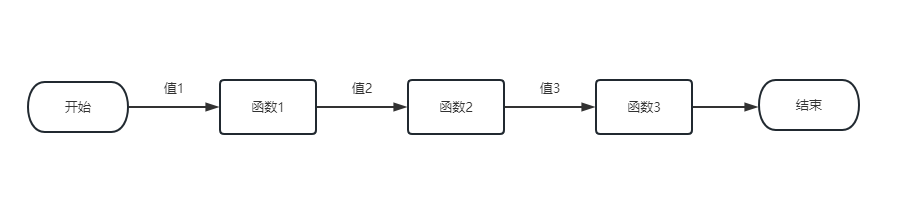
  1. totalFn 执行过程中，并不会被外部干扰。就像下图所示，我们子函数会按照我们传入的顺序执行，并把结果传入到下一个函数。直到管道所有函数执行完毕
    fnM
  2. 函数可复用性高。如果我们之后需要打 7 折，那么可以直接复用 countTotal 函数，然后重新构造管道 compose 即可。
js
function discounts7 = (price) {
    return price * 0.7
}

const totalFn = compose(countTotal, discounts7)
totalFn(shop)

这一套下来我们可以很清晰的看到函数式编程除了组合外还有 2 个特点：

  1. 函数必须是高阶函数，只有是高阶函数我们才能实现函数的组合。所以高阶函数是函数式编程的基础
  2. 函数必须是纯函数。如果函数不是纯函数，那么无法预料函数执行过程对外界产生了什么影响。

组合函数实现 ​

这种像水流过管道一样，通过一个个管口，并不被外界干扰，最终流出我们想要的水的特性就是声明式数据流

fnM

实现声明式的数据流方式有两种，一个是链式调用，另一个是组合函数。

链式 ​

接下来我们先看个链式实现声明式的数据流方式的例子：

js
function add(a) {
    return a + 4
}

function filterNum(d) {
    return d > 5
}

const arr = [1, 2, 3, 4]
const newArr = arr.map(add).filter(filterNum)

上面代码我们解决了 map 和 filter 调用完后返回数组的特性从而实现了链式调用。其中数据 arr 先留到 map 函数，再到 filter 函数，不但符合声明式数据流的特性，也符合组合函数的定义。

没错，链式其实也可以看成是组合函数的实现。只不过链式有很大的局限性：

  1. map filter 等它们都挂载在 Array 原型的 Array.prototype 上
  2. 它们在计算结束后都会 return 一个新的 Array

组合函数的实现 ​

想要实现组合函数其实很简单，我们只需要借助 reduce 函数就能很容易的实现。

回想以下 reduce 的操作流程是怎么样的？

  1. 传入一个初始值
  2. 然后对 reduce 的数组的值进行一个个的操作，并且每次操作后都需要 return 一个值给下一次

那如果我调用 reduce 的数组是保存多个函数的数组([fn1, fn2].reduce)呢？是不是就完美符合组合函数的特点了。

fnM

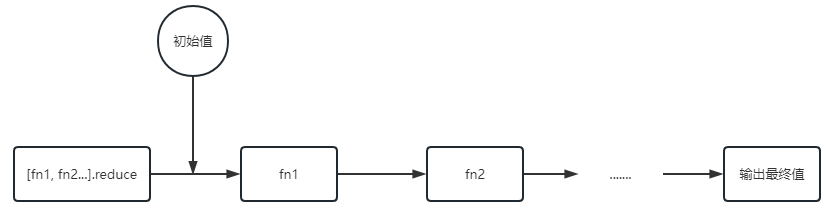
竟然了解来的 reduce 的强大，那么代码实现如下：

js
function pipe(...funcs) {
    // reduce 传入函数的返回值(prev = val, cur = func, index, arr)
    function callback(val, func) {
        return func(val)
    }  

    return function(param) {
        return funcs.reduce(callback, param)
    }
}

function add(a) {
    return a + 4
}

function multiply(c) {
    return c * 5
}
const compose = pipe(add, multiply)
console.log(compose(2)) // 30

当然上面还不是组合函数 compose，compose 跟 pipe 相比区别是 compose 则用于创建一个倒序的函数传送带。

js
function compose(...funcs) {
    // reduce 传入函数的返回值(prev = val, cur = func, index, arr)
    function callback(val, func) {
        return func(val)
    }  

    return function(param) {
        return funcs.reduceRight(callback, param)
    }
}

我们只要使用 reduceRight 倒过来即可。

缺点 ​

对组合函数来说，它总是预期链上的函数是一元函数：函数吃进一个入参，吐出一个出参，然后这个出参又会作为下一个一元函数的入参......参数个数的对齐，是组合链能够运转的前提。

一旦链上乱入了多元函数，那么多元函数的入参数量就无法和上一个函数的出参数量对齐，进而导致执行错误。

TIP

组合函数就只是一个概念。就像上面例子一样，我们可以编写一个 compose 函数来把每个单独功能的纯函数组合起来执行。也可以使用链式法则来实现纯函数组合执行。

函数柯里化 ​

函数式编程另一个特例就是柯里化。

不过在介绍函数柯里化之前，我们得先了解什么是偏函数

偏函数 ​

偏函数是指通过固定函数的一部分参数，生成一个参数数量更少的函数的过程。也就是讲一个 n (n 个入参)元函数变成一个 m(m<n) 元函数

一个四元函数

js
func(a, b, c, d)

固定参数 a，那么就变成一个三元函数

js
func(b, c, d)

或者固定参数 a、b，使其变成一个二元函数

js
func(c, d)

总之，只要它的元比之前小，就满足了偏函数的要求。

而函数柯里化就是把 1 个 n 元函数改造为 n 个相互嵌套的一元函数的过程。也就是说柯里化是一个把 fn(a, b, c)转化为fn(a)(b)(c)的过程。也就是说偏函数的实现就是函数柯里化。

代码实现 ​

函数柯里化的代码实现并不难，核心思想分两步走：

  1. 利用闭包的特性将我们每次传入的参数保存起来
  2. 判断参数是否足够，不够就继续返回柯里化函数(curry)，否则就运行传入的函数。
js
function curry(fn, args, length) {
    length = length || fn.length
    args = args || []
    return function() {
        // 保存每次调用时的入参
        args = args.concat([].slice.call(arguments))
        // 判断剩余的入参是否达到要求
        if(arguments.length < length) {
            return curry(fn, args, length - arguments.length);
        }
        // 参数够了就运行传入的函数
        return fn(...args)
    }
}

function sum(a, b, c) {
    return a + b + c
}


let add = curry(sum)
console.log(add(1)(2)(3))  // 6

柯里化加组合函数 ​

柯里化是把多元函数变成一元函数，那不是正好能解决组合函数只能使用一元函数的缺点吗？

js
function add(a, b, c) {
    return a + b + c
}

function multiply(a, b, c) {
    return a * b * c
}
// 一元化处理
const curriedAdd = curry(add)
const curriedMultiply = curry(multiply)
// 组合函数
const compose = pipe(curriedAdd(2)(3), curriedMultiply(2)(3))

console.log(compose(1))