哈希表

什么是哈希表

哈希表又称散列表(Hash table)，是一种根据键 Key 去寻找值的数据结构。而能数组刚好能根据下标地址 Key 去寻找值，所以哈希表都是基于数组来实现。

哈希函数

在使用哈希表存储值得时候，一般都是存储键值对类型。那么每一个键值对类型应该存在数组中得那个位置呢？这就得通过哈希函数来计算出来。

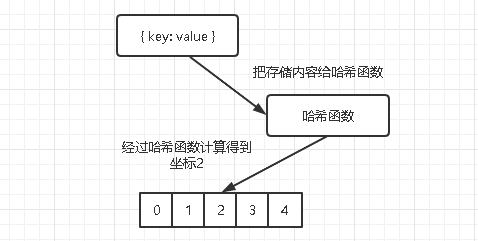
哈希函数的实现

哈希函数设计应该具备一下两个特点：

• 运算速度快
• 均匀分布

哈希表由于是通过内存地址获取值，所以速度会非常快。因此哈希函数不能采用消耗性能较高的复杂算法，否则就会得不偿失。

哈希函数应该尽量让数据均匀分布在数组中，尽量让每一个下标地址存储的内容数量相近。（注意为什么不是一个，这是应为哈希函数在计算的时候肯定会遇到计算结果一致的值）

直接定址法

h(k) = k + c
直接定址法是以关键字 k 本身加上某个常量 c。因此只适合关键字为整数切分布基本连续时的情况。

除留余数法

h(k) = k mod p
除留余数法是用关键字除以某个不大于哈希表长度的整数 p(通常取奇数比偶数好)。

TIP

以上只介绍两个常用整数的哈希函数，如果想了解更多的哈希函数的方法，请自行查找。

哈希冲突

在使用哈希函数得时候，可能会得到两个重复的值。那么如果直接复制，第二个值就会覆盖第一个，这就是哈希冲突。毕竟我们的数组长度是有限的，当值越多时，哈希冲突则越频繁。

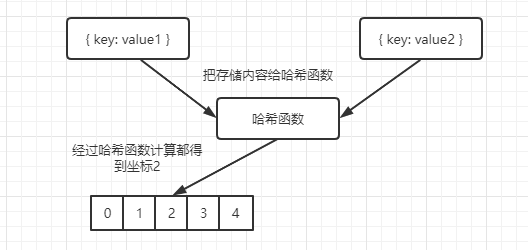
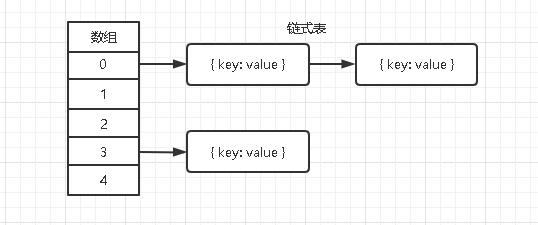
链地址法（拉链法）

拉链法其实很简单，就是在每个数组里面都存放一个链式表。这样当我们哈希函数计算出相同的下标值得时候，直接把存储内容添加到当前下标得链式表中。

开放地址法

开放地址法其主要工作方式是在发现哈希冲突的时候，就会问一问旁边的有没有空位置，有我就放在旁边，没有则继续向下问。

线性探测

从发生冲突的地址开始，依次加一向下查找，直到空位置位置。

newAddress = (oldAddress + 1) % m  // m 为哈希表的长度

线性探测法优点是解决冲突简单，但却是很容易产生堆积问题。比如第一个值占了下标为 2 的空间。那么之后如果发生冲突两次，那 3 和 4 的空间就让开放地址法给占有了。原本哈希函数映射 3 和 4 位置的值也要向后推了。

平方探测法

平方探测法则是依次进行 oldAddress + 1^2、oldAddress - 1^2、 oldAddress + 2^2、oldAddress - 2^2...这样前后查找。

newAddress = (oldAddress + i^2) % m  // m 为哈希表的长度

平方探测法能较好的处理堆积问题，但缺点时不一定能探测到哈希表上的每一个位置。